Microsoft word - pompa diamagnetica ctu 16 per depliant.doc
Approfondimento tecnico del dott. Tommaso Ferretti - relatore sulla tecnica diamagnetica al XXII congressonazionale ANASMED di medicina dello sport di Vittorio Veneto del 18-21 giugno 2006- POMPA DIAMAGNETICA SISTEMA INTEGRATO DI EROGAZIONE DI ENERGIA Premesse Nei confronti di un campo magnetico la materia ha, a seconda della sua composizione, tre comportamenti. Se ha proprietà


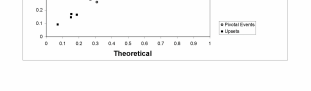 fifty elections each. The key measure of how well the theory worked is to ask how the
empirical frequency of pivotal events and upset elections compared to the prediction of
the theory. The figure above, from Levine and Palfrey [2007], plots the theoretical
predictions on the horizontal axis and the empirical frequencies on the vertical axis. It
should be emphasized that there are no free parameters – the theory is not fit to the data,
rather a direct computation is made from the parameters of the experiments. If the theory
worked perfectly the observations would align perfectly on the 45 degree line. As can be
This example of theory that works is but one of many. Other examples are double
oral auctions [Plott and Smith, 1978], and more broadly competitive environments [Roth
et al, 1991], as well as games such as best-shot [Prasnikar and Roth, 1992].
fifty elections each. The key measure of how well the theory worked is to ask how the
empirical frequency of pivotal events and upset elections compared to the prediction of
the theory. The figure above, from Levine and Palfrey [2007], plots the theoretical
predictions on the horizontal axis and the empirical frequencies on the vertical axis. It
should be emphasized that there are no free parameters – the theory is not fit to the data,
rather a direct computation is made from the parameters of the experiments. If the theory
worked perfectly the observations would align perfectly on the 45 degree line. As can be
This example of theory that works is but one of many. Other examples are double
oral auctions [Plott and Smith, 1978], and more broadly competitive environments [Roth
et al, 1991], as well as games such as best-shot [Prasnikar and Roth, 1992].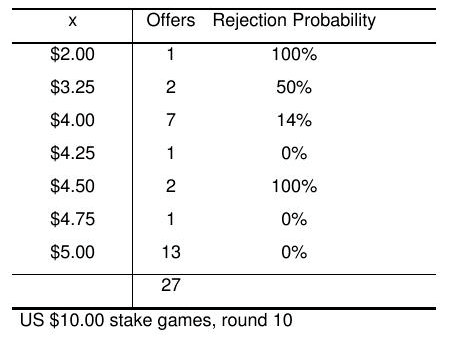 equilibrium must occur whatever the history of past play. In particular, in ultimatum
bargaining, if the second player is selfish, he must accept any offer that gives him more
than zero. Given this, the first player should ask for – and get – at least $9.95.
equilibrium must occur whatever the history of past play. In particular, in ultimatum
bargaining, if the second player is selfish, he must accept any offer that gives him more
than zero. Given this, the first player should ask for – and get – at least $9.95.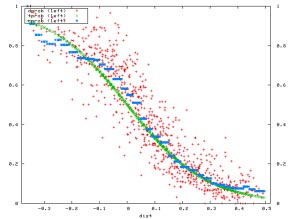 weak compared to economic factors, but in certain types of games that may make a great
To get a sense of the limitations of existing theory, it is useful to take a look under
the hood of the voting game described above. At the aggregate level the model predicts
with a high degree of accuracy. However, as anyone who has ever looked at raw
experimental data can verify, individual play is very noisy and poorly described by the
theory. The figure below from Palfrey and Levine [2007] summarizes the play of
individuals. The optimal play for an individual depends on the probability of being
pivotal (deciding the election) and on the cost of participation. The horizontal axis
measures the loss from participating depending on the cost that is drawn. If – in the given
election – the cost drawn should make the player indifferent to participating, the loss is
zero. Otherwise it can be negative or positive, depending on how much is lost from
participating. The vertical axis is the empirical probability of participating. The red dots
are the results of individual elections. The blue dots are averages of the red dots for each
loss level, and the green curve is a theoretical construct described below. The theory says
that this “best response” function should be flat with the probability of participating equal
to one until gains (negative losses) reach zero on the horizontal axis, then a vertical line,
then again flat with a value of zero for all losses that are bigger than zero. This is far from
the case: some players make positive errors, some make negative errors. The key is that
in this voting game, the errors tend to offset each other. Over voting by one voter causes
other voters to want to under vote, so aggregate behavior is not much effected by the fact
that individuals are not behaving exactly as the theory predicts. A similar statement can
be made about a competitive auction and other games in which equilibrium is strong and
robust. By way of contrast, in ultimatum bargaining, a few players rejecting bad offers
changes the incentives of those making offers, so that they will wish to make lower offers
– moving away from the subgame perfect equilibrium, not towards it.
weak compared to economic factors, but in certain types of games that may make a great
To get a sense of the limitations of existing theory, it is useful to take a look under
the hood of the voting game described above. At the aggregate level the model predicts
with a high degree of accuracy. However, as anyone who has ever looked at raw
experimental data can verify, individual play is very noisy and poorly described by the
theory. The figure below from Palfrey and Levine [2007] summarizes the play of
individuals. The optimal play for an individual depends on the probability of being
pivotal (deciding the election) and on the cost of participation. The horizontal axis
measures the loss from participating depending on the cost that is drawn. If – in the given
election – the cost drawn should make the player indifferent to participating, the loss is
zero. Otherwise it can be negative or positive, depending on how much is lost from
participating. The vertical axis is the empirical probability of participating. The red dots
are the results of individual elections. The blue dots are averages of the red dots for each
loss level, and the green curve is a theoretical construct described below. The theory says
that this “best response” function should be flat with the probability of participating equal
to one until gains (negative losses) reach zero on the horizontal axis, then a vertical line,
then again flat with a value of zero for all losses that are bigger than zero. This is far from
the case: some players make positive errors, some make negative errors. The key is that
in this voting game, the errors tend to offset each other. Over voting by one voter causes
other voters to want to under vote, so aggregate behavior is not much effected by the fact
that individuals are not behaving exactly as the theory predicts. A similar statement can
be made about a competitive auction and other games in which equilibrium is strong and
robust. By way of contrast, in ultimatum bargaining, a few players rejecting bad offers
changes the incentives of those making offers, so that they will wish to make lower offers
– moving away from the subgame perfect equilibrium, not towards it.