La tГ©tracycline, connue sous le nom commercial Sumycin, agit en bloquant la fixation de lвҖҷARNt sur la sous-unitГ© 30S ribosomale, interrompant lвҖҷГ©longation de la chaГ®ne protГ©ique bactГ©rienne. Ce mГ©canisme confГЁre une activitГ© sur un spectre large, incluant bactГ©ries Gram positives, Gram nГ©gatives, rickettsies et spirochГЁtes. Sa biodisponibilitГ© digestive varie selon la prise alimentaire et les interactions avec les ions divalents comme calcium et magnГ©sium. Sa diffusion tissulaire est importante, notamment dans les voies respiratoires et gГ©nito-urinaires. LвҖҷГ©limination se fait par voie rГ©nale et biliaire. Les effets indГ©sirables incluent photosensibilisation, troubles digestifs et coloration dentaire en cas dвҖҷadministration prГ©coce. Les guides thГ©rapeutiques mentionnent sumycin prix , en soulignant la nГ©cessitГ© de restreindre son utilisation afin de limiter les rГ©sistances acquises.
/home/journal/dvi/apa0949-apa-final-print.dvi
Appl. Phys. A 74, 779вҖ“782 (2002)/ Digital Object Identifier (DOI) 10.1007/s003390100949
Applied Physics A Materials
Science & Processing
Chemical-bond analysis of the nonlinear optical properties of the 3
O 5
, CsLiB 6
O 10
, and CsB 3
O 5
D. Xue вҲ—
, K. Betzler вҲ—вҲ—
, H. Hesse
Fachbereich Physik, UniversitГӨt OsnabrГјck, 49069 OsnabrГјck, Germany
Received: 20 February 2001
/ Accepted: 14 June 2001
/ Published online: 30 August 2001 вҖ“ пЈ© Springer-Verlag 2001
Abstract. The second-order nonlinear optical properties of
connected in different ways to form typical B
x O
y infrastruc-
practical borate crystals, LiB3O5, CsLiB6O10, and CsB3O5,
tures [8]. These various structural possibilities for the boron
which all contain the identical basic structural unit [the
atom are one of the main reasons for the crystallographic ver-
( B3O7
) 5вҲ’ group], have been quantitatively studied from the
satility of borates. The basic [BO3]3вҲ’ and [BO4]5вҲ’ groups are
chemical-bond viewpoint. Differences in the nonlinear opti-
noncentrosymmetric, the larger combined infrastructures and
cal properties among these three borate crystals arise from the
the crystals formed also often lack a center of symmetry. Such
contributions of the different cations, i.e., the different inter-
a noncentrosymmetric structure is one of the indispensable
action between the cation and the
( B3O7
) 5вҲ’ anionic group.
prerequisites for nonvanishing third-order property tensors
The chemical-bond method quantitatively expresses this im-
governing most nonlinear optical and similar applications of
portant difference. At the same time, the current calculation
materials (
ПҮijk or
dijk for second-order NLO tensors,
rijk for
also shows that the B3O7 group is a very important crys-
Pockels tensors, etc.). Due to these special features of the bo-
tallographic frame in the crystalline borate solids; it offers
rate groups, the probability of finding noncentrosymmetric
different cations an excellent coordination environment.
crystal structures in the family of borate crystals is more thantwice as high as in other crystal families [9]. In addition, bo-
PACS: 78.20.Bh; 42.65.-k; 42.65.An
rate crystals usually have the advantages of a low-absorptionand high-transmission region extending from ultraviolet toinfrared, as well as a high optical damage threshold and rea-sonable NLO coefficients, etc. [3, 10].
The origin of the optical nonlinearities of nonlinear optical
In the current work, we study the second-order NLO
(NLO) materials is one of the most interesting subjects in the
properties of three important borate crystals: LiB3O5 (LBO),
area of nonlinear optics; a comprehensive understanding has
CsLiB6O10 (CLBO), and CsB3O5 (CBO), starting from the
been intensively pursued by many research groups. Various
chemical-bond viewpoint [6]. Structurally, these three crys-
theoretical methods starting from MillerвҖҷs empirical rule up to
tals contain the same basic unit, the
( B3O7
) 5вҲ’ anionic group,
the current first-principles calculations вҖ“ at different approxi-
the importance of which has been discussed, for example, by
mation levels and from different starting points [1вҖ“6] вҖ“ have
Chen et al. [3], and they only differ in their different cations.
been more or less successfully applied to this problem. How-
Published experimental data for the second-order NLO tensor
ever various controversies still exist, for example, with regard
coefficients of these three crystals have shown obvious dif-
to the role of cations such as Li+ and Cs+ in the linear and
ferences [11вҖ“14]; therefore, finding a theoretical description
nonlinear optical properties in borate crystals such as lithium
for these differences will improve the understanding of the
borate and cesium borate [3вҖ“5, 7]. Therefore, further studies
respective materials and finally facilitate the search for new
In borate crystals, the boron atom usually coordinates
with either three or four oxygen atoms forming [BO3]3вҲ’ or[BO4]5вҲ’ groups. Accordingly, the electronic orbitals of the
1 Theoretical method
boron atoms are hybridized forming
sp 2 structures with trig-onal symmetry or
sp 3 structures exhibiting tetrahedral sym-
As shown in previous works (for an overview see [6]), the
metry. Moreover, several of these two kinds of groups can be
chemical-bond method regards certain macroscopic physicalproperties of a crystal as the combination of the contribu-
вҲ—
Present address: Institute of Chemistry, University of Ottawa, Canada
tions of all constituent chemical bonds. A multibond crystal
A
a B
b . . . is split up into constituent bonds AвҖ“B with appro-
(Fax: +49-541
/ 969-12636, E-mail: klaus.betzler@uni-osnabrueck.de)
priately chosen partial charges which can be deduced from
the detailed chemical-bonding structures of atoms A and B in
be adjusted to describe the linear susceptibility exactly. Thus
the crystal. The distribution of the valence electrons of con-
in general also the results for the nonlinear susceptibility are
stituent atoms over the contributing bonds is defined by the
so-called bond-valence equation which is formally derived
The description of the second-order nonlinear susceptibil-
from the bond graph of the compound [15].
ity can be derived in a similar way; this was basically done by
To obtain the (isotropic) linear susceptibility of a crystal
Levine [2]; extensions for complex crystals were developed
material, the contributions of all individual scalar linear bond
by Xue and Zhang [6]. The final result for the second-order
susceptibilities have to be summed up. To obtain the nonlin-
nonlinear optical tensor coefficients
dij can be written as the
ear susceptibility, the individual tensorial nonlinear bond sus-
appropriate geometric sum over the contributions of all con-
ceptibilities have to be summed up, now geometrically. The
results thus obey automatically the symmetry rules for third-
rank tensors and, moreover, the so-called Kleinman symme-
The macroscopic linear susceptibility of a crystal is given
s( 2
s вҲ’ 1
)(r ) 2
f
by the sum over all contributions and can be written as
The first part denotes the ionic fraction, the second part
the covalent fraction of the nonlinear optical coefficient.
The meaning of the constants on the right-hand side of (6)
fraction of bonds of type
Вө composing the crystal;
geometrical contribution of chemical bonds of type
Вө ;
linear susceptibility contribution from
Вө type bonds;
number of bonds of type
Вө per cm3;
number of bonds of type
Вө per cm3;
susceptibility of a single bond of type
Вө .
susceptibility of a single bond of type
Вө ;
Z ) вҲ—,
(Z ) вҲ—: effective number of valence electrons
According to Phillips [17] and Van Vechten [18] the lin-
ear susceptibility
ПҮВө contributed by the bonds of type
Вө in
ПҮВө =
( 4
ПҖ) вҲ’1
(hв„ҰВө/EВө) 2
,
f i ,
f c : fractions of ionic and covalent characteristics
p is the plasma frequency and
E g is the average en-
=
(CВө) 2
/(E g
) 2 and
f c =
(E h
ergy gap between the bonding and antibonding states of the
bond length of the
Вө type bonds in Г…;
bond.
E g can be separated into homopolar and heteropolar
(i.e., covalent and ionic) contributions
E and
CВө
exponent in the bond force constant (2.48);
r c = 0
. 35
r : core radius, where
r =
dВө/ 2;
EВө) 2 =
(E ) 2 +
(CВө) 2
,
=
( Вө вҲ’
Вө)/( Вө +
Вө)
r and
r are the covalent radii of atoms A and B.
All of the above constants have to be deduced from a struc-
CВө =
K 2
bВө exp
( вҲ’
kВөr ) (Z ) вҲ— вҲ’
n(Z ) вҲ—
tural analysis based on the crystallographic structure and tak-
ing into account the detailed chemical-bonding situation of all
1 and
K 2 are constants consisting only of funda-
mental physical constants such as
h, e , etc., and adapted to
constituent atoms [6]. It should be emphasized that besides
the units of measure used in the concrete calculation (for
the parameter
ОІ , introduced for the linear susceptibility, no
lengths in Г… and energies in eV, the numerical values are
further adjustable parameters are included.
K 1 = 39
. 74 and
K 2 = 14
. 4 [19]).
dВө = 2
r is the bond length
of the
Вө -type bond AвҖ“B; exp
( вҲ’
k s
r ) is the ThomasвҖ“Fermi
2 Results and discussion
screening factor.
(Z ) вҲ— and
(Z ) вҲ— are the effective numbers
of valence electrons of the two atoms in the bond,
n is the
The three crystals discussed here вҖ“ LBO, CLBO and CBO вҖ“
ratio of the numbers of the two elements B and A in the
are structurally closely related due to their similar atomic ar-
bond-valence equation [7, 20]. Because the true screening be-
rangement. Starting from LBO, for example, a complete sub-
haviour in a solid is more complex than this simple ThomasвҖ“
stitution of Li by Cs yields CBO, a partial substitution (50%)
Fermi description, a correction factor
bВө is introduced [18].
yields CLBO. LBO belongs to the orthorhombic space group
This factor is also used to correct for
d -electron influences
Pna 21 with unit cell dimensions
a = 8
. 4473
, b = 7
. 3788,
not accounted for in the effective
Z вҲ—. These
d -electron ef-
and
c = 5
. 1395 [23]; CLBO crystallizes in the tetragonal
fects on the bond susceptibilities were at first considered by
space group
I 42
d with unit cell dimensions
a = 10
. 494
, c =
Levine [19] but are still in controversial discussion [21, 22].
8
. 939 [24]; CBO is in the orthorhombic space group
P 212121
According to LevineвҖҷs conclusion [2], the different factors
bВө
with unit cell dimensions
a = 6
. 213
, b = 8
. 521, and
c =
can be written as
bВө =
ОІ( ВҜ
N c
) 2, with one global parameter,
9
. 170 [25]. Each of these three crystals has 36 atoms, i.e.,
ОІ вҖ“ global for all of the different bonds in the compound вҖ“
N c is the average coordination number of the ions
CsLiB6O10, respectively, in one unit cell. The detailed struc-
A and B in the bond
Вө . If the linear susceptibility, i.e., the
tural properties of LBO have already been discussed in a pre-
refractive index, of a crystal is known, this parameter
ОІ can
vious publication [7]; therefore we will mainly concentrate
Table 1. Chemical-bond parameters of constituent chemical bonds of CLBO
Table 2. Chemical-bond parameters of constituent chemical bonds of CBO
Fig. 1. Li and Cs cations around the (B3O7)5вҲ’ anionic group in CLBO.
Atomic positions are labeled according to the bond designations in Table 1
here on the other two compounds. Their structural arrange-
ment is shown in Figs. 1 and 2. One of the four symmetry-
equivalent basic
( B3O7
) 5вҲ’ anionic groups in the unit cell вҖ“
together with representative cations вҖ“ is sketched in Fig. 1 for
CLBO and in Fig. 2 for CBO. As in LBO, two (BO
4
) 5вҲ’ tetrahedral group form a slightly dis-
torted six-member BвҖ“O ring, sharing corner oxygen ions. The
additional bonds, different for each compound, are introduced
Starting from the chemical-bonding structures of all con-
stituent atoms in each crystal, we have quantitatively calcu-lated the chemical-bond parameters of all constituent chem-
and by Sasaki et al. for CBO [25]. The calculated results
ical bonds, and further all independent second-order NLO
for CLBO and CBO are summarized in Tables 1 and 2; de-
tensor coefficients
dij of these three crystals possessing dif-
tailed results for LBO have been published in a previous
ferent cations and the same
( B3O7
) 5вҲ’ anionic group. For
the calculations we used the structural data measured by
As already discussed for LBO [7], the calculations show
Ihara et al. for LBO [23], by Krogh-Moe for CLBO [24]
that the
( B3O7
) 5вҲ’ structural unit is of great importance for theNLO properties of all three compounds. This is in good agree-ment with the conclusions on NLO borates with (B3O7)5вҲ’groups derived using the so-called anionic group theory [3].
In all three crystals, the central structural unit (B3O7)5вҲ’ is ofnearly identical size. Yet there are expressed differences inthe bond covalency values and the bond susceptibilities forthis anionic group between the three crystals. This indicatesthat not only the influence of the anionic groups but also thatof the cations, i.e., the contributions of all constituent bonds,have to be considered thoroughly. Different ions at the cationsites seem to affect the NLO properties of the LBO familycrystals quite strongly.
Two main effects can be clearly stated from the data calcu-
lated: (a) cations with lower electronegativity values (Cs: 0.7,Li: 1.0) reduce the bond covalency values in the anionic groupwhen replacing Li; (b) CsвҖ“O bonds introduce higher bondsusceptibilities than LiвҖ“O bonds.
These effects, especially the second one, finally lead to an
increase in the NLO susceptibility such that
d LBO
< d CLBO
< d CBO
.
Our results for the NLO susceptibilities are summarized in
Fig. 2. Cs cations around the (B
Table 3 together with experimental data and data calculated
positions are labeled according to the bond designations in Table 2
by other schemes. The comparison shows that the chemical-
Table 3. Second-order NLO tensor coeffi-
cients
dij (in p
m ) of LBO, CLBO and CBO.
Comparison of experimental results with dif-ferent calculation schemes. LDA: local dens-ity approximation. CNDO: complete neglect
вҲ’
( 1
. 05 Вұ 0
. 13
) a
вҲ’
( 0
. 83 Вұ 0
. 06
) b
вҲ’
( 0
. 06 Вұ 0
. 004
) a
1
. 04
( 1 Вұ 0
. 2
) d
bond scheme is quite reliable for calculating linear and non-
References
1. R.C. Miller: Appl. Phys. Lett.
5 , 17 (1964)
2. B.F. Levine: Phys. Rev. B
7 , 2600 (1973)
3. C. Chen, N. Ye, J. Lin, J. Jiang, W. Zeng, B. Wu: Adv. Mater.
11 , 1071
3 Conclusion
4. W.-D. Cheng, J.-T. Chen, Q.-S. Lin, Q.-E. Zhang, J.-X. Lu: Phys. Rev.
The second-order nonlinear optical susceptibilities of three
B
60 , 11 747 (1999)
similar borate materials вҖ“ lithium borate, cesium lithium bo-
5. C. Duan, J. Li, Z. Gu, D. Wang: Phys. Rev. B
59 , 369 (1999)
6. D. Xue, S. Zhang: Physica B
262 , 78 (1999)
rate, and cesium borate вҖ“ have been quantitatively studied
7. D. Xue, S. Zhang: Appl. Phys. A
65 , 451 (1997)
from the chemical-bond viewpoint of crystal materials. The
8. D. Xue, K. Betzler, H. Hesse, D. Lammers: Solid State Commun.
114 ,
results show that as well as the anionic group
( B
which is identical for all three compounds, the different
9. G. Heller:
A survey of structural types of borates and polyborates .
Topics in Current Chemistry (Springer, Berlin 1986)
cations involved influence the susceptibility in a characteris-
10. P. Becker: Adv. Mater.
10 , 979 (1998)
tic way. Heavier cations decrease the covalency values for the
11. S. Lin, Z. Sun, B. Wu, C. Chen: J. Appl. Phys.
67 , 634 (1990)
bonds in the anionic group and increase the susceptibility of
12. S.P. Velsko, M. Webb, L. Davis, C. Huang: IEEE J. Quantum Electron.
the cationвҖ“oxygen bond. Especially the latter leads to an in-
QE-27 , 2182 (1991)
crease in the resulting macroscopic susceptibility induced by
13. Y. Wu, T. Sasaki, S. Nakai, A. Yokotani, H. Tang, C. Chen: Appl. Phys.
Lett.
62 , 2614 (1993)
14. Y. Mori, I. Kuroda, S. Nakajima, T. Sasaki, S. Nakai: Appl. Phys. Lett.
The present work shows that heavier cations strengthen
67 , 1818 (1995)
the interaction between the cation and the
( B3O7
) 5вҲ’ anionic
15. I.D. Brown: Acta Cryst. B
48 , 553 (1992)
group. From the chemical-bond viewpoint, the crystals can be
16. D.A. Kleinman: Phys. Rev.
126 , 1977 (1962)
considered to consist of two parts, the fundamental structural
17. J.C. Phillips: Rev. Mod. Phys.
42 , 317 (1970)
18. J.A. van Vechten: Phys. Rev.
182 , 891 (1969)
frame of anionic groups, nearly identical for all three com-
19. B.F. Levine: Phys. Rev. B
7 , 2591 (1973)
pounds, and the individual cations, which, in addition, impose
20. D. Xue, S. Zhang: Chem. Phys.
226 , 307 (1998)
characteristic modifications on the linear and nonlinear opti-
21. H. Neumann: Cryst. Res. Technol.
24 , 815 (1989)
22. J.M. Merino, R. Diaz, M. Leon: Phys. Rev. B
61 , 10 211 (2000)
23. M. Ihara, M. Yuge, J. Krogh-Moe: Yogyo-Kyokai-Shi
88 , 179 (1980)
24. J. Krogh-Moe: Acta Cryst. B
30 , 1178 (1974)
Acknowledgements. Dr. Xue thanks the Alexander von Humboldt Founda-
25. T. Sasaki, Y. Mori, I. Kuroda, S. Nakajima, K. Yamaguchi, S. Watan-
tion for all the support during his stay in Germany.
abe, S. Nakai: Acta Cryst. C
51 , 2222 (1995)
Source: http://crystech.com.cn/cn/discuss/lit9.pdf
Prefeitura Municipal de Santiago MUNICГҚPIO DE SANTIAGO - RS EDITAL DE PREGГғO ELETRГ”NICO NВә 8/2010 PROCESSO ADMINISTRATIVO NВә 2858/2010 MANUTENГҮГғO DAS ATIVIDADES DA SECRETARIA MUNICIPAL DE SAГҡDE" O PREFEITO MUNICIPAL DE SANTIAGO, no uso de suas atribuiГ§Гөes, TORNA PГҡBLICO, para conhecimento dos interessados, que se encontra aberta licitação na modalidade PREGГғO ELETRГ
BГ•RGYГ“GYГҒSZAT AJГҒNLГҒS AZ ACNE VULGARIS KEZELГүSГүHEZ вҖў Semmelweis Egyetem ГҒOK, BГөr-, NemikГіrtani Г©s BГөronkolГіgiai Klinika Munkacsoportja вҖў 3. LOKГҒLIS FAGGYГҡMIRIGY-MГӣKГ–DГүST bГөrbetegsГ©g, a 11 Г©s 30 Г©v kГ¶zГ¶tti serdГјlГөk Г©s CSГ–KKENTГ• SZEREK fiatal felnГөttek csaknem 80%-ГЎt Г©rinti. Nincs jelenleg a piacon ilyen hatГЎsГә lokГЎlisPatomechanizmusГЎban 4 fГө
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
0-9



 Appl. Phys. A 74, 779вҖ“782 (2002)/ Digital Object Identifier (DOI) 10.1007/s003390100949
Applied Physics A
Appl. Phys. A 74, 779вҖ“782 (2002)/ Digital Object Identifier (DOI) 10.1007/s003390100949
Applied Physics A




 the detailed chemical-bonding structures of atoms A and B in
be adjusted to describe the linear susceptibility exactly. Thus
the crystal. The distribution of the valence electrons of con-
in general also the results for the nonlinear susceptibility are
stituent atoms over the contributing bonds is defined by the
so-called bond-valence equation which is formally derived
The description of the second-order nonlinear susceptibil-
from the bond graph of the compound [15].
the detailed chemical-bonding structures of atoms A and B in
be adjusted to describe the linear susceptibility exactly. Thus
the crystal. The distribution of the valence electrons of con-
in general also the results for the nonlinear susceptibility are
stituent atoms over the contributing bonds is defined by the
so-called bond-valence equation which is formally derived
The description of the second-order nonlinear susceptibil-
from the bond graph of the compound [15].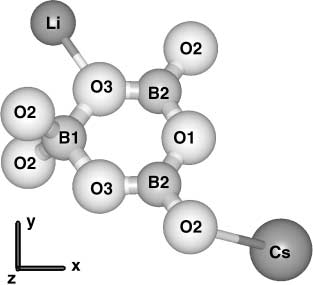
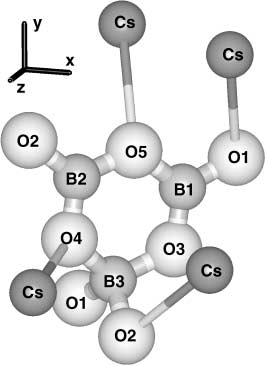







 Table 1. Chemical-bond parameters of constituent chemical bonds of CLBO
Table 1. Chemical-bond parameters of constituent chemical bonds of CLBO


 Table 3. Second-order NLO tensor coeffi-
Table 3. Second-order NLO tensor coeffi-